Under the influence of a gravitational field, a differential temperature applied to opposite sides of a cavity causes buoyancy-driven convective flow. In practical analysis, the specification of a heat transfer convection coefficient drives the modeling of natural convection. However, high sensitivity to the chosen constant convection coefficient is a source of error for heat transfer analysis. Hence, the idea of this numerical study is to model convection coupling the following:
- Navier Stokes Equations – Conservation of momentum
- Advection-Diffusion Equation – Conservation of thermal energy
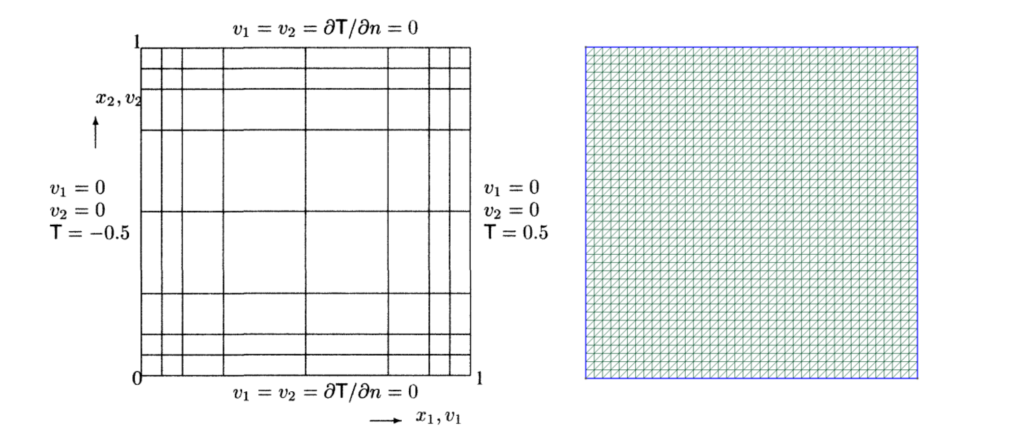
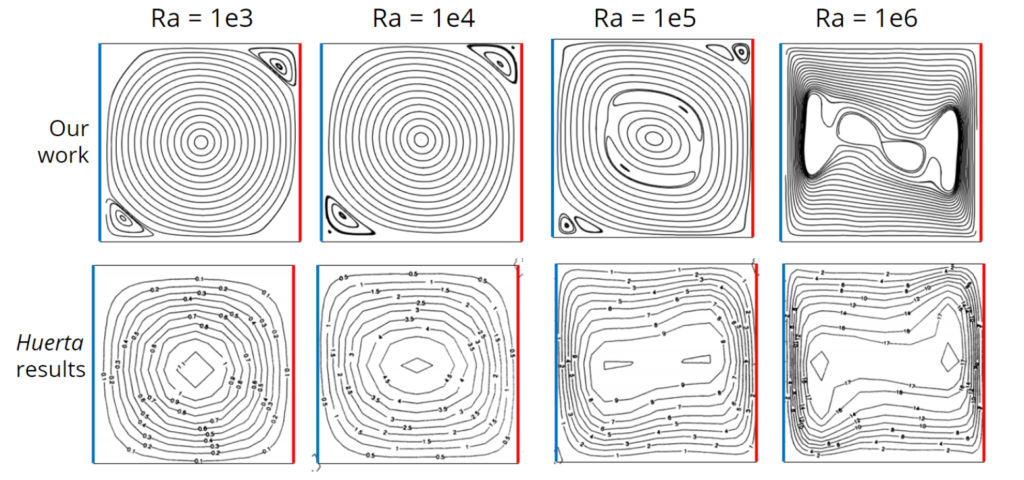
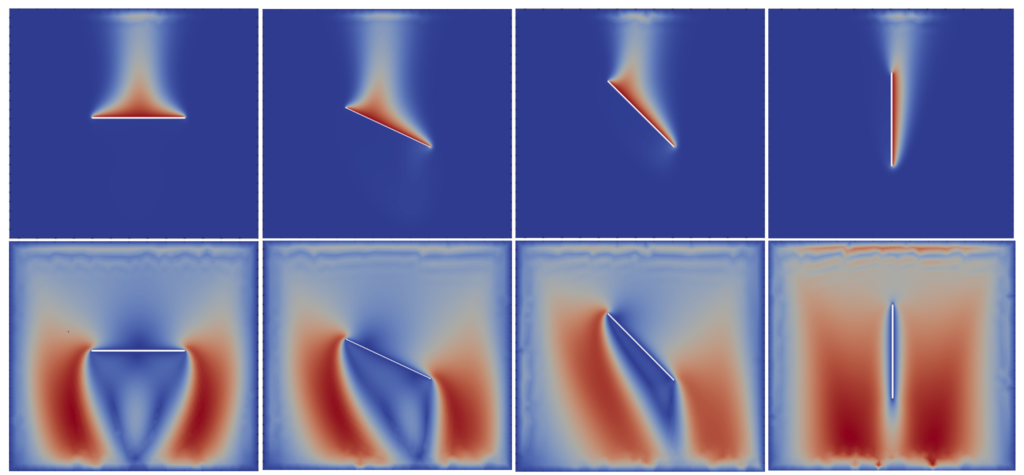
The initial validation of the solution of equations was conducted by simulating a steady recirculating flow in a square cavity. After the solution was validated, the main study focused on a practical engineering application: analyzing the natural convective flow around a heated plate geometry (a good use case would be, for example, estimating the convection from inclined
solar panel.)
The final problem was implementing Unsteady Convection in a Differential Heated Cavity using Monolithic Solve solution algorithm.